Fast Calibration of Car Following Models to Trajectory Data Using the Adjoint Method
/Abstract
Before a car-following model can be applied in practice, it must first be validated against real data in a process known as calibration. This paper discusses the formulation of calibration as an optimization problem and compares different algorithms for its solution. The optimization consists of an arbitrary car following model, posed as either an ordinary or delay differential equation, being calibrated to an arbitrary source of trajectory data that may include lane changes. Typically, the calibration problem is solved using gradient free optimization. In this work, the gradient of the optimization problem is derived analytically using the adjoint method. The computational cost of the adjoint method does not scale with the number of model parameters, which makes it more efficient than evaluating the gradient numerically using finite differences. Numerical results are presented that show that quasi-Newton algorithms using the adjoint method are significantly faster than a genetic algorithm and also achieve slightly better accuracy of the calibrated model.
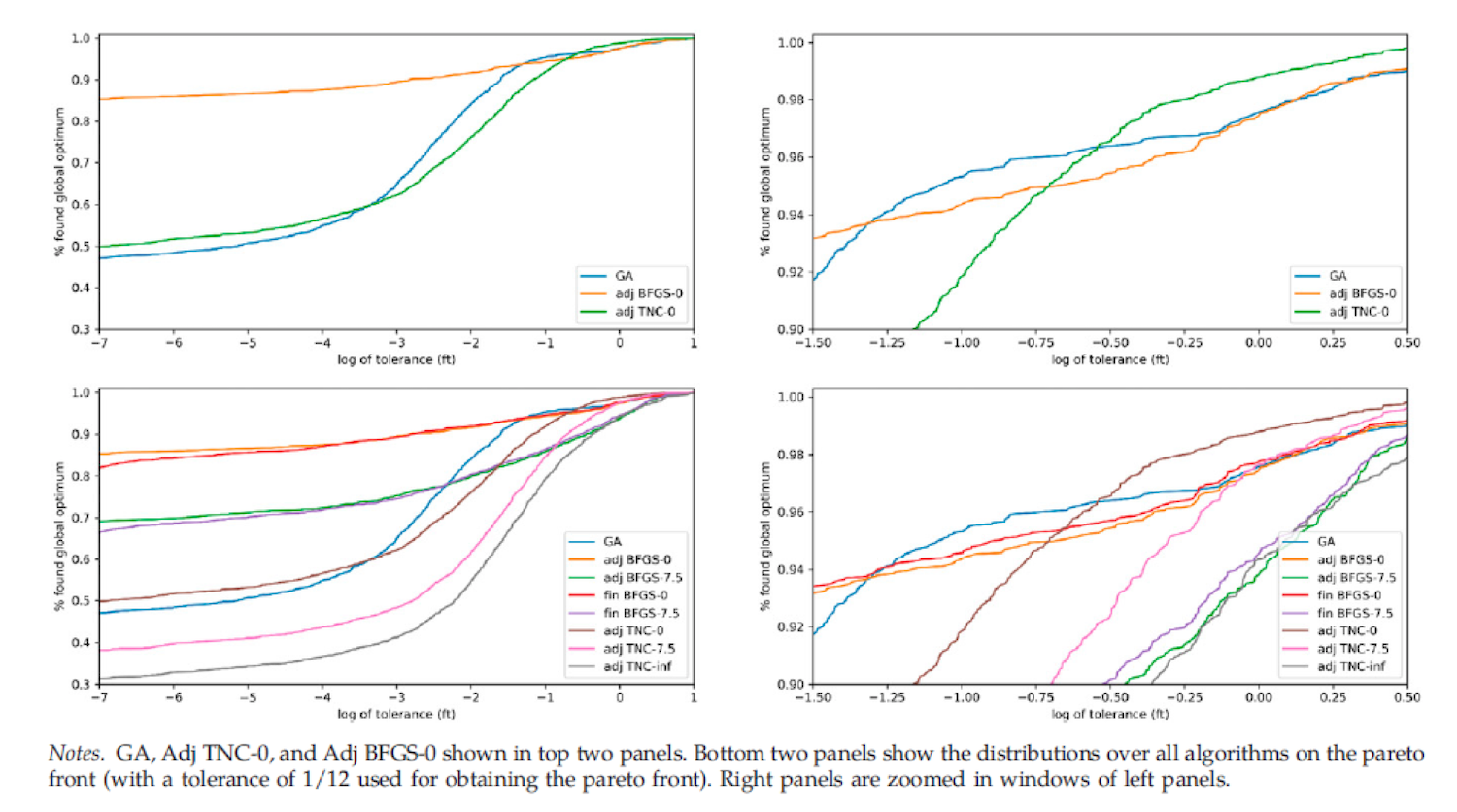
Distributions of RMSE over the global optimum for different algorithms